Chat Overview

Rumelhart et al. (1986) - Backpropagation

The 1986 revival of backpropagation by Rumelhart, Hinton, and Williams enabled deep learning by allowing neural networks to learn internal representations through gradient-based optimization.

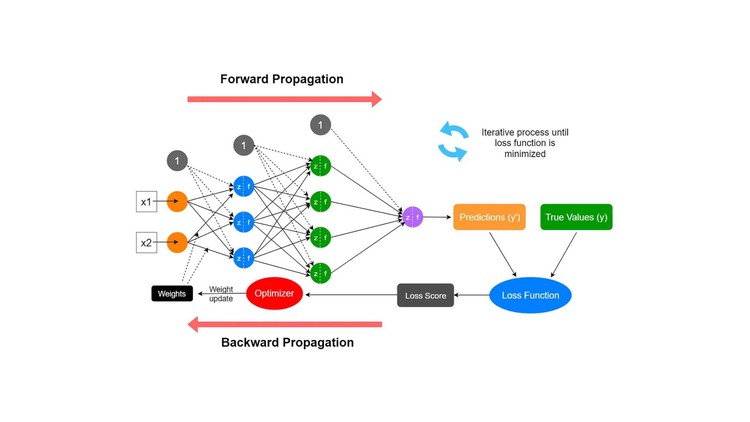
/images/foundations/backprop-diagram.jpg
Backpropagation allows multi-layer networks to learn by adjusting weights via error gradients.

The 1986 paper by David Rumelhart, Geoffrey Hinton, and Ronald Williams marked a turning point in the history of neural networks. Their work reintroduced and popularized the backpropagation algorithm, which made it possible to train multi-layer neural networks - overcoming the severe limitations of the earlier Perceptron model.

By enabling internal layers to learn distributed representations, backpropagation laid the mathematical foundation for modern deep learning.

Historical Context

In the decades following Rosenblatt’s Perceptron , neural network research lost momentum. A major reason was the discovery that single-layer models could not solve simple non-linear problems like XOR. The publication of Perceptrons by Minsky and Papert (1969) emphasized this flaw and ushered in an “AI winter” for connectionist approaches.

Rumelhart et al. built on earlier ideas from control theory and automatic differentiation to formalize an efficient way to compute gradients through multiple layers of weights. Their 1986 paper, Learning representations by back-propagating errors, demonstrated empirically that neural networks could be trained to perform nontrivial tasks by adjusting weights through error propagation.

Technical Summary

Backpropagation is a supervised learning algorithm based on gradient descent. The key idea is to minimize a loss function by propagating the error signal from the output layer backward through the network:

Key Steps:

  1. Forward pass: Compute the output of the network for a given input.
  2. Loss computation: Measure the difference between the prediction and the true label.
  3. Backward pass: Use the chain rule of calculus to compute gradients of the loss with respect to each weight.
  4. Update weights: Adjust weights using gradient descent.

Example weight update rule:

w := w - η \* (dL/dw)

Where:

  • w is a weight in the network
  • η is the learning rate
  • dL/dw is the partial derivative of the loss with respect to the weight

This approach enabled networks to learn internal representations, allowing them to extract features at multiple levels of abstraction.

Key Contributions

  • Multi-layer learning: Solved the XOR problem by enabling hidden layers to transform data non-linearly.
  • General-purpose framework: Applicable to classification, regression, and sequence tasks.
  • Scalable: Backprop is the basis for training modern architectures like CNNs , LSTMs , and Transformers .

Impact and Legacy

Backpropagation ignited the resurgence of interest in neural networks, setting the stage for the deep learning revolution. It formed the backbone of models like Deep Belief Nets , which introduced unsupervised pretraining, and eventually large-scale architectures like GPT .

Despite criticisms - such as its biological implausibility and sensitivity to initialization - backprop remains the standard training method for artificial neural networks. Its influence is visible across nearly every modern model covered in our evolution overview .

Further Reading

  • Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533–536.
  • LeCun et al. (1998). Gradient-based learning applied to document recognition. Proc. IEEE.
  • Background in Rosenblatt (1958) and Turing (1950)